[알고리즘] 자료구조란?(배열,스택,큐,해시테이블,힙)/JAVA코드

👩🏻‍🏫 자료구조란?

개발자가 데이터를 효율적으로 사용할 수 있도록 정리한 방법

🔎 자료구조 종류

1. Array(배열)

크기가 고정되어 있다
동일한 데이터 타입만 저장 가능
Index(0-n) / Elements

import java.util.Scanner;
 
public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in); //입력
        
        int N = sc.nextInt();
        int[] arr = new int[N]; //배열 생성
        
        for(int i=0; i<N; i++) {
            arr[i] = sc.nextInt(); //배열에 값 입력
        }
    }
}

2. 스택

후입선출 (FILO)
한쪽에서만 자료를 넣거나 뺄 수 있다
- push(): 데이터 넣기
- pop(): 데이터 꺼내기

import java.util.Stack;

public class Main {
    public static void main(String[] args) {
        Stack<Integer> stack = new Stack<>(); //스택 생성

        stack.push(10); //push
        stack.push(20);
        stack.push(30);
        
        System.out.println("스택 크기: " + stack.size()); // 3
        System.out.println("맨 위 데이터: " + stack.peek()); // 30

        System.out.println("Pop한 데이터: " + stack.pop()); // 30
        System.out.println("Pop한 데이터: " + stack.pop()); // 20
        System.out.println("스택이 비어있는지 확인: " + stack.isEmpty()); // false
    }
}

3. 큐

선입선출 (FIFO)
- Enqueue(인큐): 데이터 넣기
- Dequeue(디큐): 데이터 꺼내기

import java.util.LinkedList;
import java.util.Queue;

public class QueueExample {
    public static void main(String[] args) {
        Queue<Integer> queue = new LinkedList<>(); // 큐 생성

        queue.offer(10); // enqueue
        queue.offer(20);
        queue.offer(30);

        int item = queue.poll(); // dequeue
        System.out.println("Dequeued item: " + item);

        int frontItem = queue.peek(); // peek: 큐의 프론트(front) 항목 참조
        System.out.println("Front item: " + frontItem);

        boolean isEmpty = queue.isEmpty(); // isEmpty: 큐가 비어 있는지 확인
        System.out.println("Is queue empty? " + isEmpty);

        int size = queue.size(); // size: 큐의 크기 확인
        System.out.println("Queue size: " + size);
    }
}

4. 해시테이블

key, value 쌍으로 데이터 저장

import java.util.HashMap;

public class HashTableExample {
    public static void main(String[] args) {
    
        HashMap<String, Integer> hashTable = new HashMap<>(); // Hash Table 생성

        hashTable.put("A", 1); //데이터 추가
        hashTable.put("B", 2);
        hashTable.put("C", 3);

        int valueA = hashTable.get("A"); //데이터 조회
        System.out.println("Value of A: " + valueA);

        hashTable.remove("B"); // 데이터 삭제
        
        boolean containsC = hashTable.containsKey("C"); // 데이터 유무 확인
        System.out.println("Contains C: " + containsC);

        // 모든 키-값 쌍 순회
        for (String key : hashTable.keySet()) {
            int value = hashTable.get(key);
            System.out.println("Key: " + key + ", Value: " + value);
        }
    }
}

5. 그래프

node사이에 edge가 있다

6. 트리

그래프가 계층적 구조를 가진 형태
- Root: 최상위 노드
- Parent node(부모 노드): 상위 노드
- Child node(자식 노드): 하위 노드
Biary Search Tree(이진 탐색 트리)
- 왼쪽 자식노드 키 값 < 부모노드 키 값 < 오른쪽 자식노드 키 값

이진트리 코드

class TreeNode {
    private int data;
    private TreeNode left;
    private TreeNode right;
    
    public TreeNode(int data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
    
    public int getData() {
        return data;
    }
    
    public void setData(int data) {
        this.data = data;
    }
    
    public TreeNode getLeft() {
        return left;
    }
    
    public void setLeft(TreeNode left) {
        this.left = left;
    }
    
    public TreeNode getRight() {
        return right;
    }
    
    public void setRight(TreeNode right) {
        this.right = right;
    }
}

class BinaryTree { //이진 트리
    private TreeNode root;
    
    public BinaryTree() {
        root = null; // 이진 트리의 루트 노드 초기화
    }
    
    public boolean isEmpty() {
        return root == null; // 이진 트리가 비어 있는지 여부 반환
    }
 }

검색 코드

    public boolean search(int data) { //데이터 검색
        return searchNode(root, data); 
    }
    
    private boolean searchNode(TreeNode current, int data) {
        if (current == null) {
            return false; // 현재 노드가 null인 경우 데이터를 찾지 못한 것이므로 false를 반환.
        }
        
        if (data == current.getData()) {
            return true; // 현재 노드의 데이터와 찾는 데이터가 일치하면 true를 반환
        } else if (data < current.getData()) {
            return searchNode(current.getLeft(), data); // 데이터가 현재 노드의 데이터보다 작으면 왼쪽 자식을 탐색
        } else {
            return searchNode(current.getRight(), data); // 데이터가 현재 노드의 데이터보다 크면 오른쪽 자식을 탐색
        }
    }
}

삽입 코드

    public void insert(int data) {
        root = insertNode(root, data); // 데이터를 이진 트리에 삽입
    }
    private TreeNode insertNode(TreeNode current, int data) {
        if (current == null) {
            current = new TreeNode(data); // 현재 노드가 null인 경우 새로운 노드 생성
        } else {
            if (data <= current.getData()) {
                current.setLeft(insertNode(current.getLeft(), data)); // 데이터가 현재 노드의 데이터보다 작거나 같으면 왼쪽 자식에 삽입
            } else {
                current.setRight(insertNode(current.getRight(), data)); // 데이터가 현재 노드의 데이터보다 크면 오른쪽 자식에 삽입
            }
        }
        return current;
    }

삭제 코드

    public void delete(int data) { //삭제
        root = deleteNode(root, data);
    }
    
    private TreeNode deleteNode(TreeNode current, int data) {
        if (current == null) {
            return null; // 현재 노드가 null인 경우 삭제할 데이터를 찾지 못한 것이므로 null 반환
        }
        
        if (data == current.getData()) {
            // 삭제할 노드가 단말 노드인 경우
            if (current.getLeft() == null && current.getRight() == null) {
                return null; // 왼쪽과 오른쪽 자식이 없는 단말 노드를 삭제하고 null 반환
            }
            // 삭제할 노드가 오른쪽 자식만 가지는 경우
            else if (current.getLeft() == null) {
                return current.getRight(); // 오른쪽 자식을 현재 노드로 대체
            // 삭제할 노드가 왼쪽 자식만 가지는 경우
            else if (current.getRight() == null) {
                return current.getLeft(); // 왼쪽 자식을 현재 노드로 대체
            }
            // 삭제할 노드가 양쪽 자식을 가지는 경우
            else {
                int smallestValue = findSmallestValue(current.getRight()); // 오른쪽 서브트리에서 가장 작은 값을 찾는다
                current.setData(smallestValue); // 삭제할 노드의 데이터를 찾은 가장 작은 값으로 대체
                current.setRight(deleteNode(current.getRight(), smallestValue)); // 가장 작은 값을 가진 노드를 삭제
                return current;
            }
        } else if (data < current.getData()) {
            current.setLeft(deleteNode(current.getLeft(), data)); // 데이터가 현재 노드의 데이터보다 작으면 왼쪽 자식 삭제
            return current;
        } else {
            current.setRight(deleteNode(current.getRight(), data)); // 데이터가 현재 노드의 데이터보다 크면 오른쪽 자식 삭제
            return current;
        }
    }
    
    private int findSmallestValue(TreeNode root) {
    	// 오른쪽 서브트리에서 가장 작은 값을 찾기 위해 왼쪽 자식으로 계속 이동한다.
        return root.getLeft() == null ? root.getData() : findSmallestValue(root.getLeft());
    }

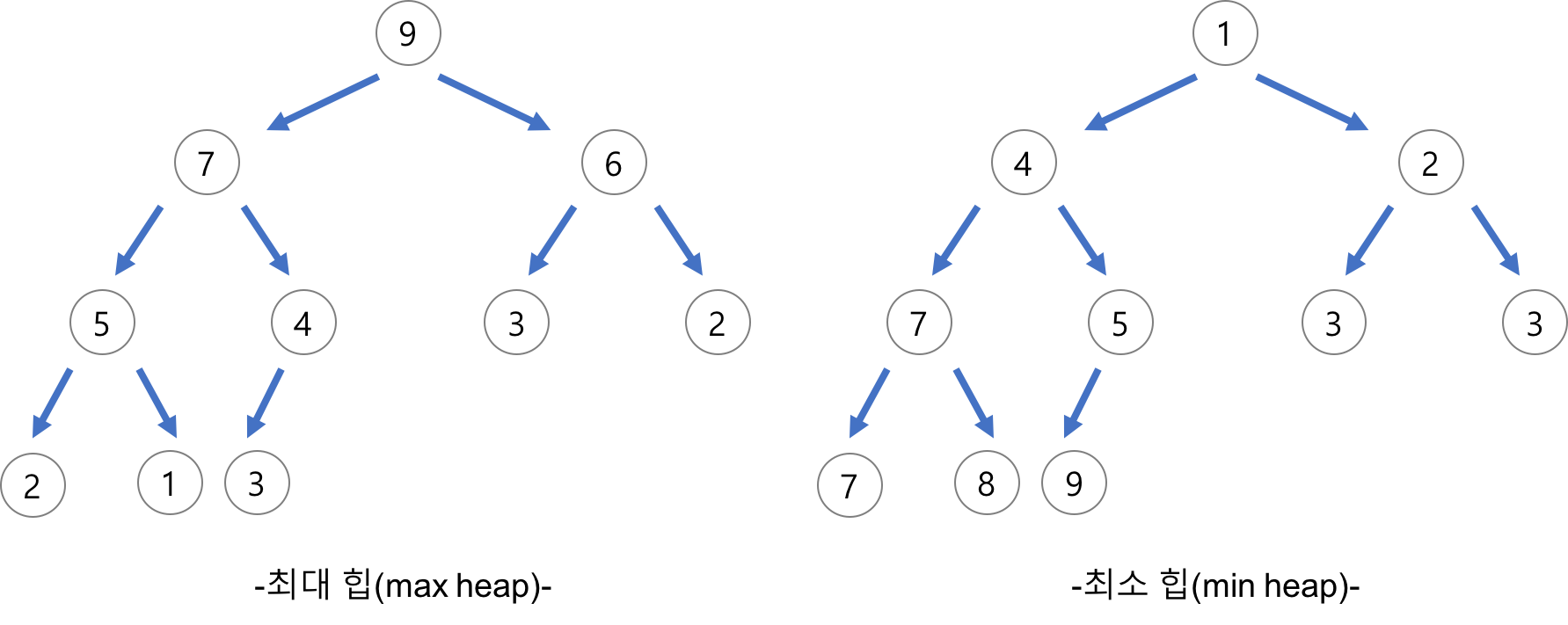
7. Heap(힙)

완전 이진 트리의 일종
max heap(최대 힙)
- 부모 노드의 키 값 >= 자식 노드의 키 값
min heap(최소 힙)
- 자식 노드의 키 값 >= 부모 노드의 키 값

index
- 1부터 사용
- 왼쪽 자식 인덱스 = 부모 인덱스 * 2
- 오른쪽 자식 인덱스 = 부모 인덱스 * 2 + 1

import java.util.PriorityQueue;

public class HeapExample {
    public static void main(String[] args) {
        PriorityQueue<Integer> minHeap = new PriorityQueue<>(); // 최소 힙 생성

        minHeap.offer(5); //삽입
        minHeap.offer(2);
        minHeap.offer(8);
        minHeap.offer(1);

        int minValue = minHeap.peek(); // 최소값
        System.out.println("Min value: " + minValue); // 1

        int deletedValue = minHeap.poll(); //(최소값) 삭제
        System.out.println("Deleted value: " + deletedValue); // 1 삭제
    }
}

📃 백준 문제집

1. 연산

https://www.acmicpc.net/workbook/view/8997

2. 자료구조

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

자바공부하기

[알고리즘] 자료구조란?(배열,스택,큐,해시테이블,힙)/JAVA코드

👩🏻‍🏫 자료구조란?

🔎 자료구조 종류

1. Array(배열)

2. 스택

3. 큐

4. 해시테이블

5. 그래프

6. 트리

7. Heap(힙)

📃 백준 문제집

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역